CNN Basics and Modern Architecture

August 17, 2024 6 minute read

卷积神经网络（CNN）是深度学习发展过程中不可忽视的重要结构之一，在图像处理领域，是以深度学习为基础的方法的基础结构。本文意在梳理CNN的基本原理和现代演进结构，巩固基础，展望未来。

从全连接网络(FCN)到卷积神经网络(CNN)

全连接神经网路（Fully connected network）没有对特征之间如何交互有任何假设，每一个神经元都与其他所有神经元有连接。当处理表格类型的数据时（e.g. 图像），一个$10^6$像素的图像，即使做Reduction操作，和1000维的隐藏层做全连接，需要$10^6 \times 10^e = 10^9$个参数，当网络更加复杂时，数据量更大时，参数量将会剧烈增加，训练网络需要更多的资源、耐心和技巧。

图像数据本身包含丰富的结构信息，当人类区分图片中的动物是猫或狗时，不会逐个检查每个像素之间的关系，而是利用图像块之间的关系和信息来识别，相邻的像素包含相似的语义信息（Locality），图像语义块之间的关系不会变换(Translation Invariance)。卷积神经网络(Convolution neural network)，系统化的利用Locality和Invariance，可以使用更少的参数学习到有用的信息：

在浅层网络中，网路应该关注局部区域(Locality)，不用关系其他区域的内容；对于同一个区域，不论其处在图片中的哪个位置，网络应该要作出相似的反应(Translation Invariance/Equivariance)。
深层网络，汇聚浅层网络的信息，捕捉图片中长距离的特征间的关系。

改造MLP为CNN

MLP关注每个像素和其他所有像素的关系，每个像素和其他所有像素之间都存在权重。考虑二维输入图片 $X$ 和 $H$ 二维隐藏层权重 $H_{i,j}$, $X_{i,j}$分别图片和隐藏层表示位置(i,j)处的像素, $U_{i,j}$代表bias：

\[\begin{aligned} \left[\mathbf{H}\right]_{i, j} &= [\mathbf{U}]_{i, j} + \sum_k \sum_l[\mathsf{W}]_{i, j, k, l} [\mathbf{X}]_{k, l}\\ &= [\mathbf{U}]_{i, j} + \sum_a \sum_b [\mathsf{V}]_{i, j, a, b} [\mathbf{X}]_{i+a, j+b}.\end{aligned}\]

在第二行，对公式做改写，并对下标重新索引，令$k=i+1, l=j+b$，因此 $\mathbf{V}_{i,j,a,b}=\mathbf{W}_{i,j,i+a,j+b}$，通过改变a和b的范围，就能覆盖整张图像，做到全连接。

Notice: $\mathbf{W}$在MLP中一般表示为二维权重，此处用四维权重是为了表达让隐藏层的每一个神经元都能接受到来自输入图像的每一个像素，因此每一个隐藏层的神经元都有一个二维权重矩阵，神经元之间的权重矩阵不共享。一个 1000 x 1000的输入图像映射到 1000 x 1000的隐藏层，需要 $10^{12}$的参数量。

利用Translation Invariance

平移不变性暗示平移输入X，在隐藏层H中也会有相应的平移。即：在U和V都不依赖于位置(i,j)时, 才平移不变性才可能发生。因此，让$\mathbf{V}_{i,j,a,b}=\mathbf{V}_{a,b}$, $U$是常量u,因此H可简化为：

\[[\mathbf{H}]_{i, j} = u + \sum_a\sum_b [\mathbf{V}]_{a, b} [\mathbf{X}]_{i+a, j+b}.\]

这就是卷积！权重V不再依赖图像中的位置变量(i,j)，所需参数量 $4 \times 10^6$。(why 4?)。此时 a 和 b的取值范围是 [-1000, 1000]，接下来需要利用局部性原理限制a和b的取值范围。

利用Locality

局部性原理表明，隐藏层中位置(i,j)出的值之和输入中(i,j)的邻域有关系，因此a和b的取值需要限制在一定的范围内，超过范围，$\mathbf{V}_{a,b}=0$。

\[[\mathbf{H}]_{i, j} = u + \sum_{a = -\Delta}^{\Delta} \sum_{b = -\Delta}^{\Delta} [\mathbf{V}]_{a, b} [\mathbf{X}]_{i+a, j+b}.\]

参数量为$4 \times \Delta^2$，$\Delta$通常小于10。$V$被叫做可学习的卷积核，滤波器或者权重。至此，参数量从$10^12$降低到$4\Delta^2$，这是一个巨大的下降。

卷积通道

基于MLP改造的卷积层，输入和输出都只有一个通道，实际上，图片有长、宽、通道数量三种维度，为了表达更多维度，隐藏层也可以拥有很多通道维度，来捕捉通道之间的特征。因此卷积核$\mathbf{V}_{a,b}$需要表示为$\mathbf{V}_{a,b,c,d}$，c,d分别表示输入和输出通道下标。

\[[\mathsf{H}]_{i,j,d} = \sum_{a = -\Delta}^{\Delta} \sum_{b = -\Delta}^{\Delta} \sum_c [\mathsf{V}]_{a, b, c, d} [\mathsf{X}]_{i+a, j+b, c},\]

实现卷积

Notice：上文描述的操作严格来说不是卷积，而是互相关性，本质上他们的计算结果是相同的，遵从深度学习的术语，我们仍称其为卷积。详见Cross-Correlation and Convolution

忽略通道量，在二维图像$(n_h \times n_w)$上卷积，卷积核 $(k_h \times k_w)$，输出维度为$(n_h-k_h+1) \times (n_w-k_w+1)$

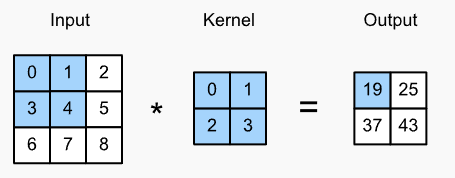
二维卷积图示

\[0\times0+1\times1+3\times2+4\times3=19,\\ 1\times0+2\times1+4\times2+5\times3=25,\\ 3\times0+4\times1+6\times2+7\times3=37,\\ 4\times0+5\times1+7\times2+8\times3=43.\]

# Pytorch implementation
def corr2d(X, K):
    """Compute 2D cross-correlation."""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y


# Conv2d Layer
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

特征图(Feature Map): 卷积层的输出的通常称谓。
感受野(Receptive Field): 影响某层l中的神经元x的输出值的前l-1层的所有元素。

Padding 和 Stride

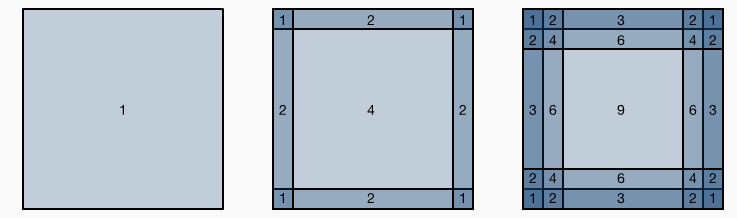
使用卷积时，图像边缘的像素信息会一定程度丢失，卷积核越大，图片边缘的信息丢失越严重。如下图所示，卷积核为1x1, 2x2, 3x3时，图片边缘的像素点的使用次数。单次卷积虽然损失不大，但随着网络的加深，累计效应会放大。

直接的解决方法：输入四周补充像素点，补充的像素点设置为0。例如下图

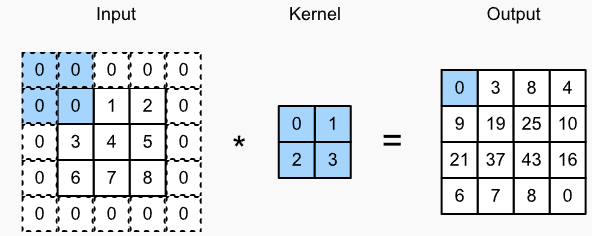
pading样例

增加padding后，卷积输出shape变为：

\[(n_\textrm{h}-k_\textrm{h}+p_\textrm{h}+1)\times(n_\textrm{w}-k_\textrm{w}+p_\textrm{w}+1).\]

在许多应用中，为了让输入输出shape一致，$p_h = k_h - 1, p_w = k_w - 1$，这样更容易预估输出的shape。当 $k_h$为奇数时，我们将会在两边添加$\frac{p_h}{2}$列，当 $k_h$为偶数时，一种pad方式是在左边增加$\lceil p_\textrm{h}/2\rceil$，右边增加$\lfloor p_\textrm{h}/2\rfloor$列。

通常，CNN使用高和宽为奇数的卷积核，这样可以让pad的行数或者列数在图片上下左右相同，保持维度大小、比例不变。

执行卷积操作时，卷积核每次移动一步。我们也可以移动多步，以增加计算效率或者想做下采样。当卷积核很大的时候，可以捕捉更大的区域，此时，我们可以适当增加移动步长。

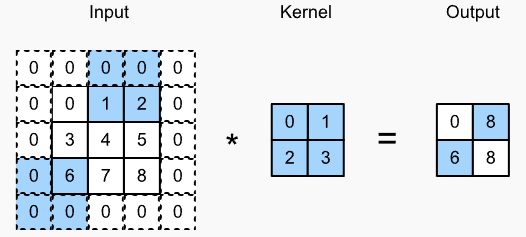
conv_stride

strides of 3 and 2 for height and width

当stride $(s_h,s_w)$被设置后，卷积的输出shape为： $\lfloor(n_\textrm{h}-k_\textrm{h}+p_\textrm{h}+s_\textrm{h})/s_\textrm{h}\rfloor \times \lfloor(n_\textrm{w}-k_\textrm{w}+p_\textrm{w}+s_\textrm{w})/s_\textrm{w}\rfloor.$

当 $p_h = k_h - 1, p_w = k_w - 1$时，卷积输出shape为：

\[\lfloor(n_\textrm{h}+s_\textrm{h}-1)/s_\textrm{h}\rfloor \times \lfloor(n_\textrm{w}+s_\textrm{w}-1)/s_\textrm{w}\rfloor\]

当输入的宽和高可以被stride整除，卷积输出shape为：

\[(\frac{n_h}{s_h} \times \frac{n_w}{s_w})\]

多通道输入输出卷积实现

多通道输入-单通道输出卷积

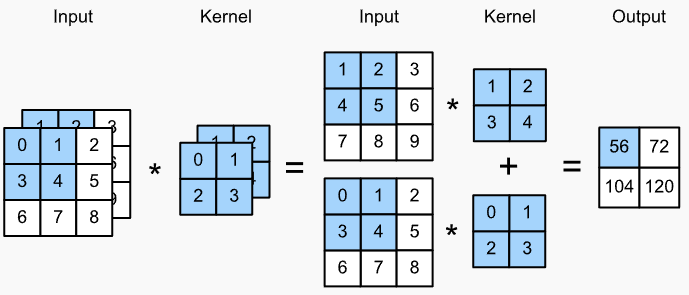
multi_input_channel

两个输入通道的卷积计算，卷积核也同样具有两个通道，分别对应输入的两个通道，每个通道卷积的结果相加，作为最终结果, e.g. $(1\times1+2\times2+4\times3+5\times4)+(0\times0+1\times1+3\times2+4\times3)=56$.

# Pytorch Implementation
def corr2d_multi_in(X, K):
    # Iterate through the 0th dimension (channel) of K first, then add them up
    return sum(corr2d(x, k) for x, k in zip(X, K))

多通道输入-多通道输出卷积

$c_i, c_o$分别为输入输出的通道数量，卷积核的shape为 $c_o \times c_i \times k_h \times k_w$。卷积结果是concat起来每个输出通道对应的卷积核和所有的输入通道做卷积。

# Pytorch implementation
def corr2d_multi_in_out(X, K):
    # Iterate through the 0th dimension of K, and each time, perform
    # cross-correlation operations with input X. All of the results are
    # stacked together
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)

$1 \times 1$卷积核

$1 \times 1$卷积核在单通道卷积中没有作用，它不能让输出神经元看到输入的相邻区域。在多通道输入中，$1\times1$卷积可以在channel维度做计算，相当于在channel维度做全连接，因此它需要的参数量为$c_i \times c_o$

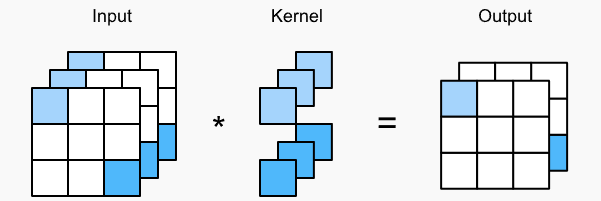
conv_1x1

三输入channel, 两输出channel，$1\times1$卷积图

def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    X = X.reshape((c_i, h * w))
    K = K.reshape((c_o, c_i))
    # Matrix multiplication in the fully connected layer
    Y = torch.matmul(K, X)
    return Y.reshape((c_o, h, w))

X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))
Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6 # True, Y1.shape == Y2.shape

池化

池化层没有参数，它主要两个作用：

减缓卷积对局部的敏感, 网络越深，隐藏层元素的感受野越大，就更敏感
空间下采样，降低空间分辨率，加速计算

常用两种池化层：

平均池化(Average Pooling)：将局部区域的均值作为输出
最大池化(Maximum Pooling)：将局部区域的最大值最为输出，输出越大特征越强越能表征该局部区域的重要性，大多数case中，最大池化效果更好

def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y

对多channel输入，池化对每个channel分别生效，而不是沿着channel维度加起来。

池化层和卷积核一样，具有pad和stride参数，含义同卷积核一致。

经典CNN网络结构

From LeNet to Alexnet

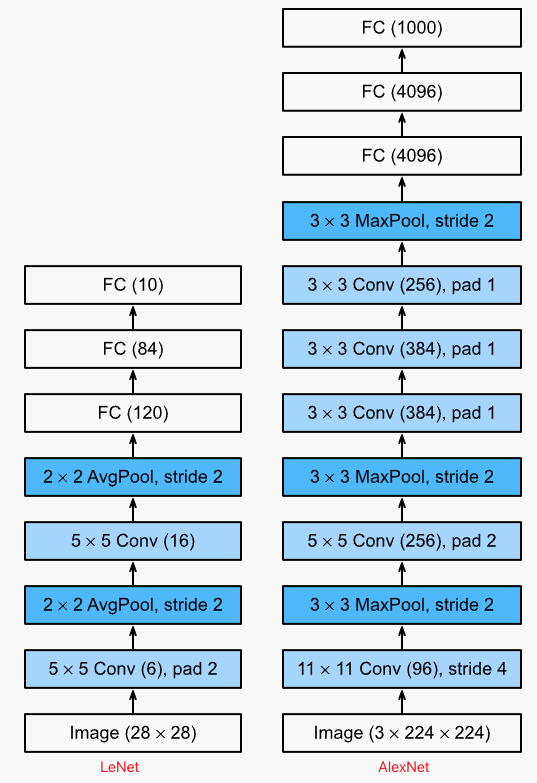
lenet_alexnet

AlexNet 卷积核更大，这主要是ImageNet图片的宽和高是MNIST图片的8倍，最后的全连接层更大，也是因为ImageNet的分类数量更多
激活函数：Sigmoid (LeNet) -> ReLU (Alexnet)
池化层：Average Pool (LeNet) -> Maximum Pool (Alexnet)
模型容量：AlexNet 模型层数更多，并采用Dropout技术控制模型负载度；LeNet则仅仅使用权重衰减。

VGG

CNN的基础构建块通常包含3步：

卷积层，同时增加Pad保持分辨率
非线性层，e.g. ReLU
池化层，降低分辨率，e.g. MaxPool

按照这种方式构建，一个224 x 224的输入图片，CNN不会拥有超过8个卷积层($log_2d$)。

VGG的解决思路：在两个下采样之间，连续使用多个卷积、非线性变换。VGG将其实现为一个VGG Block，堆叠多个VGG Block变构成了VGG Net。

其结果会导致网络加深，因此卷积核不宜使用太大的，以避免参数占用过大。用连续两个3x3卷积看到的像素区域和一个5x5卷积看到的一致，但参数量只需要$2 \times 3^2 \times c^2$，远少于 $25 \times c^2$。后续研究表明，更深、更窄的模型效果远好于同等参数量的浅层模型。此后，模型朝着更深的方向发展，3x3的卷积成为深度网络的标配置。最近的研究中，ParNet表明通过使用大量的并行计算模块，使用更浅的网络能够达到深层网路同样的效果，未来可能会对网络设计有重要的影响。

vgg

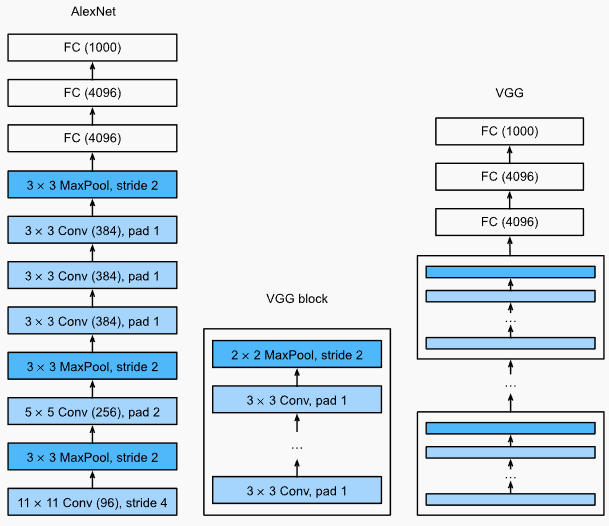
# VGG Block
def vgg_block(num_convs, out_channels):
    layers = []
    for _ in range(num_convs): # number of convs
        layers.append(nn.LazyConv2d(out_channels, kernel_size=3, padding=1))
        layers.append(nn.ReLU())
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

# VGG net
class VGG(d2l.Classifier):
    def __init__(self, arch, lr=0.1, num_classes=10):
        super().__init__()
        self.save_hyperparameters()
        conv_blks = []
        for (num_convs, out_channels) in arch:
            conv_blks.append(vgg_block(num_convs, out_channels))
        self.net = nn.Sequential(
            *conv_blks, nn.Flatten(),
            nn.LazyLinear(4096), nn.ReLU(), nn.Dropout(0.5),
            nn.LazyLinear(4096), nn.ReLU(), nn.Dropout(0.5),
            nn.LazyLinear(num_classes))
        self.net.apply(d2l.init_cnn)

NiN (Network in Network)

LetNet, AlexNet, VGG有相同的设计模式：先利用一串卷积和池化层抽取空间结构特征，后接全连接网络和具体的任务。这种设计存在两个挑战：

网络最后的全连接层参数量很大，内存占用高，无法用于小型设备
在网络前面增加全连接以增加非线性，不仅破坏图像的空间结构也会占用的内存

NiN的解决思路：

使用1x1卷积在通道之间增加局部的非线性（对每个像素在通道之间做全连接）
在网络最后的表示层中，使用全局平均池化层聚合不同位置的信息。

Notice: 如果没有通道之间的局部非线性，全局平均池化将不会有效。

nin

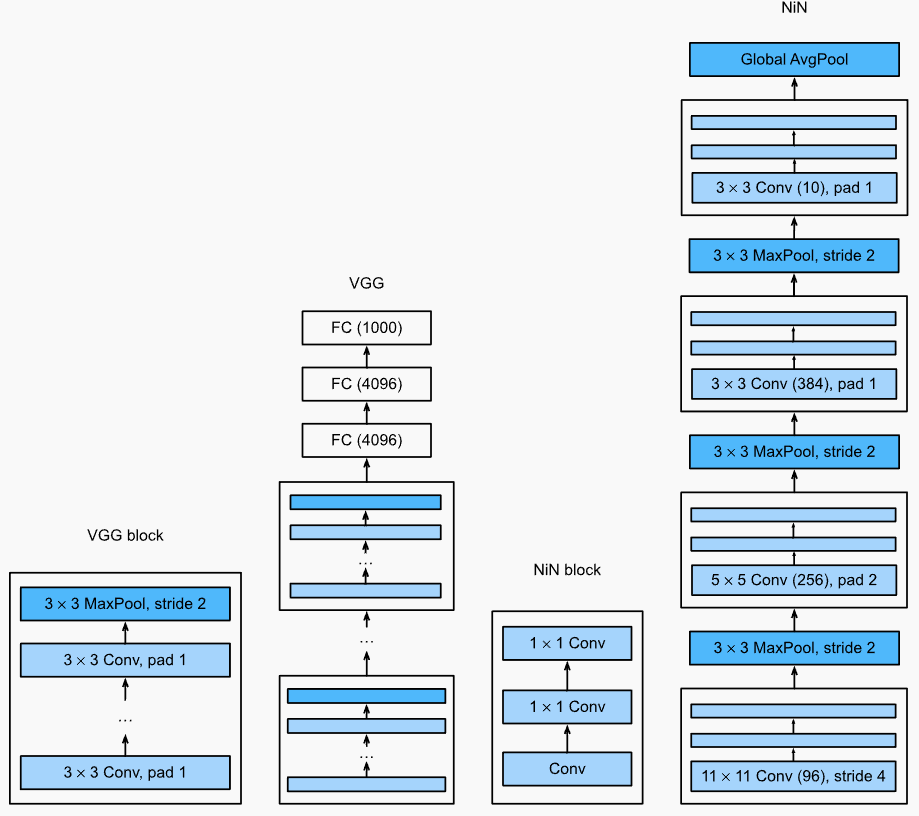
NiN同VGG有两个重要的区别：

网络最后的表示层仅使用全局平均池化层，整个网络都避免使用全连接层。
NiN Block有两个连续的1x1卷积。相比一个，连续两个1x1卷积，能够提高非线性能力，提取到更有表达力的特征，计算量也会相应增加。
网络最后的NiN块的输出通道数量和分类数量一致，产生和分类数量一致的logit向量，用于分类

NiN网络让研究者震惊的一点是：使用全局平均池化，并没有对精度有损。这是因为在低分辨率表示（有很多通道的表示）上做平均，相当于增加了一定量的平移不变性

# NiN Block
def nin_block(out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.LazyConv2d(out_channels, kernel_size, strides, padding), nn.ReLU(),
        #Notice! two consective 1x1 conv
        nn.LazyConv2d(out_channels, kernel_size=1), nn.ReLU(),
        nn.LazyConv2d(out_channels, kernel_size=1), nn.ReLU())

class NiN(d2l.Classifier):
    def __init__(self, lr=0.1, num_classes=10):
        super().__init__()
        self.save_hyperparameters()
        self.net = nn.Sequential(
            nin_block(96, kernel_size=11, strides=4, padding=0),
            nn.MaxPool2d(3, stride=2),
            nin_block(256, kernel_size=5, strides=1, padding=2),
            nn.MaxPool2d(3, stride=2),
            nin_block(384, kernel_size=3, strides=1, padding=1),
            nn.MaxPool2d(3, stride=2),
            nn.Dropout(0.5),
            nin_block(num_classes, kernel_size=3, strides=1, padding=1),
            nn.AdaptiveAvgPool2d((1, 1)),
            nn.Flatten())
        self.net.apply(d2l.init_cnn)

GoogLeNet: Multi-branch Network

GoogLeNet继承了 NiN、重复的BLock、多种卷积核混合的优点，显示对网络中各层的作用进行划分：

stem（数据消化)，主要是网络前2～3层的卷积，抽取图像的底阶表示
body (数据处理)，卷积块
head (预测)，输出用于下游任务的表示

GoogLeNet将多个卷积核并行连接，最后Concat起来，一定程度上解决了如何选取卷积核的问题。这就是该网络的基础构建块 Inception Block

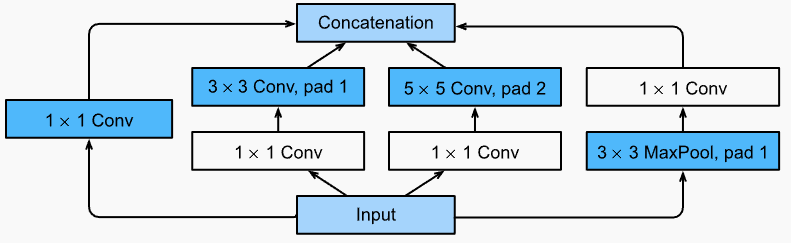
inception

不同大小的卷积核用于抽取不同空间大小的特征
1x1卷积用于缩小通道数量
MaxPool->1x1 conv，先池化后降低通道数量
四个分支的输出在通道维度上Concat起来

一个块中包含了不同大小的卷积核和池化层，用户通常需要调整的参数就是输出的通道数量，简化了卷积核选取问题。

class Inception(nn.Module):
    # c1--c4 are the number of output channels for each branch
    def __init__(self, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # Branch 1
        self.b1_1 = nn.LazyConv2d(c1, kernel_size=1)
        # Branch 2
        self.b2_1 = nn.LazyConv2d(c2[0], kernel_size=1)
        self.b2_2 = nn.LazyConv2d(c2[1], kernel_size=3, padding=1)
        # Branch 3
        self.b3_1 = nn.LazyConv2d(c3[0], kernel_size=1)
        self.b3_2 = nn.LazyConv2d(c3[1], kernel_size=5, padding=2)
        # Branch 4
        self.b4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.b4_2 = nn.LazyConv2d(c4, kernel_size=1)

    def forward(self, x):
        b1 = F.relu(self.b1_1(x))
        b2 = F.relu(self.b2_2(F.relu(self.b2_1(x))))
        b3 = F.relu(self.b3_2(F.relu(self.b3_1(x))))
        b4 = F.relu(self.b4_2(self.b4_1(x)))
        return torch.cat((b1, b2, b3, b4), dim=1)

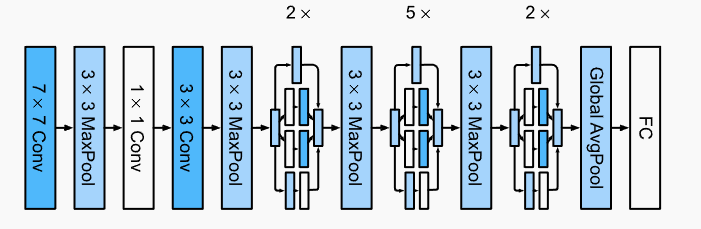
googlenet

class GoogleNet(d2l.Classifier):
    def b1(self):
        return nn.Sequential(
            nn.LazyConv2d(64, kernel_size=7, stride=2, padding=3),
            nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
    def b2(self):
        return nn.Sequential(
          nn.LazyConv2d(64, kernel_size=1), nn.ReLU(),
          nn.LazyConv2d(192, kernel_size=3, padding=1), nn.ReLU(),
          nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
    def b3(self):
        return nn.Sequential(Inception(64, (96, 128), (16, 32), 32),
                         Inception(128, (128, 192), (32, 96), 64),
                         nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
    def b4(self):
        return nn.Sequential(Inception(192, (96, 208), (16, 48), 64),
                         Inception(160, (112, 224), (24, 64), 64),
                         Inception(128, (128, 256), (24, 64), 64),
                         Inception(112, (144, 288), (32, 64), 64),
                         Inception(256, (160, 320), (32, 128), 128),
                         nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
    def b5(self):
        return nn.Sequential(Inception(256, (160, 320), (32, 128), 128),
                         Inception(384, (192, 384), (48, 128), 128),
                         nn.AdaptiveAvgPool2d((1,1)), nn.Flatten())
    def __init__(self, lr=0.1, num_classes=10):
        super(GoogleNet, self).__init__()
        self.save_hyperparameters()
        self.net = nn.Sequential(self.b1(), self.b2(), self.b3(), self.b4(),
                                self.b5(), nn.LazyLinear(num_classes))
        self.net.apply(d2l.init_cnn)

ResNet and ResNeXt

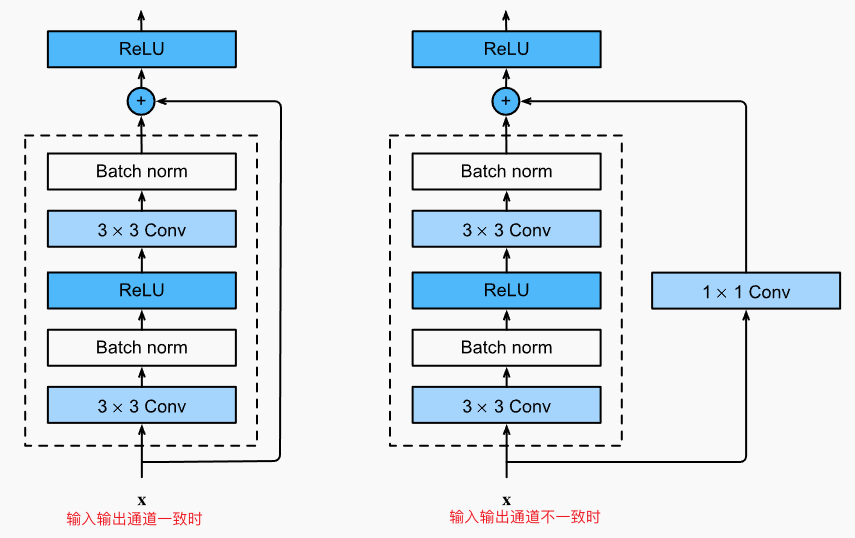
问题：增加网络层是如何增加网络的复杂度和表达性质的，而不是在增加网络层后，网络表达能力下降？

如果我们能将新增加的layer训练成$f(x)=x$，新模型将会至少和原模型一样有效，或许还能获得更好的效果。

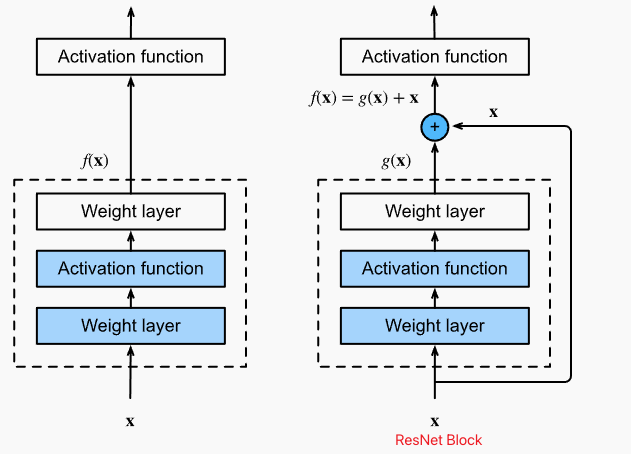
resnet block

右边虚线网络学习映射关系$g(x)=f(x)-x$，如果$f(x)=x$, $g(x)=0$，因此更容易学习，只需要让虚线网络的权重和偏置向0学习既可。

值得注意的是：残差连接在激活函数之前相加, BatchNorm在激活之前使用；另外，为了方便改变输出的通道，增加1x1卷积改变输入的通道数量保持和输出一致。

resnet1

class Residual(nn.Module):  #@save
    """The Residual block of ResNet models."""
    def __init__(self, num_channels, use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1 = nn.LazyConv2d(num_channels, kernel_size=3, padding=1,
                                   stride=strides)
        self.conv2 = nn.LazyConv2d(num_channels, kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.LazyConv2d(num_channels, kernel_size=1,
                                       stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.LazyBatchNorm2d()
        self.bn2 = nn.LazyBatchNorm2d()

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)



class ResNet(d2l.Classifier):
    def b1(self):
        return nn.Sequential(
            nn.LazyConv2d(64, kernel_size=7, stride=2, padding=3),
            nn.LazyBatchNorm2d(), nn.ReLU(),
            nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
    def block(self, num_residuals, num_channels, first_block=False):
        blk = []
        for i in range(num_residuals):
            if i == 0 and not first_block:
                blk.append(Residual(num_channels, use_1x1conv=True, strides=2)) 
            else:
                blk.append(Residual(num_channels))
        return nn.Sequential(*blk)
    def __init__(self, arch, lr=0.1, num_classes=10):
        super(ResNet, self).__init__()
        self.save_hyperparameters()
        self.net = nn.Sequential(self.b1())
        for i, b in enumerate(arch):
            self.net.add_module(f'b{i+2}', self.block(*b, first_block=(i==0)))
        self.net.add_module('last', nn.Sequential(
            nn.AdaptiveAvgPool2d((1, 1)), nn.Flatten(),
            # 注意，增加了FC层
            nn.LazyLinear(num_classes)))
        self.net.apply(d2l.init_cnn)

残差网络块设计一个痛点：需要在非线性和输出维度作出权衡：

增加非线性，可以增加网络层数、增加卷积核大小。参数量无疑会增加，这种增加方式，没有留下参数优化的余地。
增加通道数量，增加块之间携带的信息量。参数量增加正比于 $O(c_i \times c_o)$

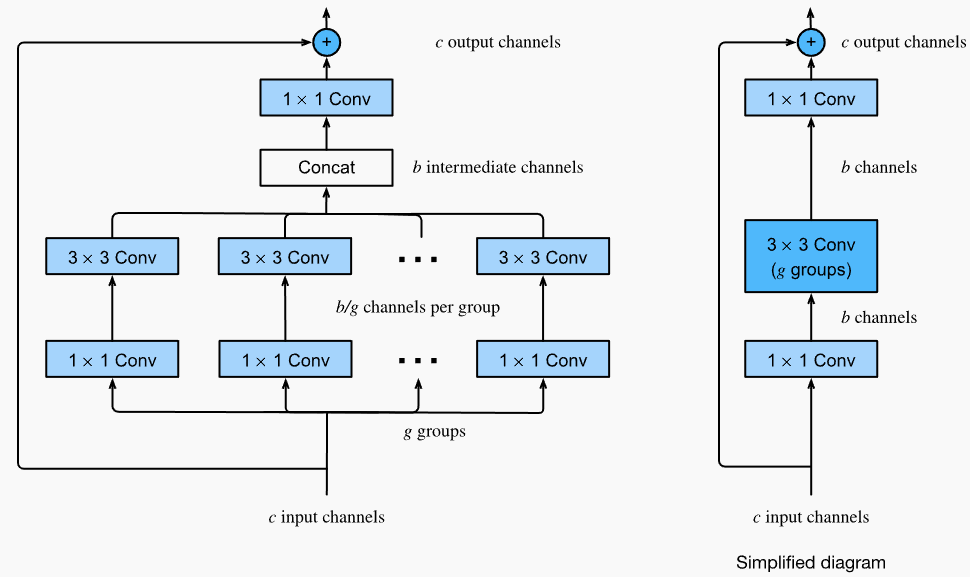
受Inception block启发，可以让残差块拥有多个相互独立的分支，不同于Inception每个分支都不相同，我们让残差的每个分支都相同，最后将分支的结果在通道维度concat起来。

分组前, 1x1卷积需要参数量$c_i \times c_o$
分组后，$g \times \frac{c_i}{g} \times \frac{c_o}{g} = \frac{c_i \times c_o}{g}$

分组后, 不同分组之间没有信息交互，ResNeXt通过将3x3的分组卷积放在两个1x1卷积之间解决，需要的参数量为 $c_i \times b + c_o \times b + \frac{b^2}{g} = b \times (c_i+c_o+\frac{b}{g})$，

res_next_block

class ResNeXtBlock(nn.Module):  #@save
    """The ResNeXt block."""
    def __init__(self, num_channels, groups, bot_mul, use_1x1conv=False,
                 strides=1):
        super().__init__()
        bot_channels = int(round(num_channels * bot_mul)) # b
        self.conv1 = nn.LazyConv2d(bot_channels, kernel_size=1, stride=1) # 1x1, c_i x b
        self.conv2 = nn.LazyConv2d(bot_channels, kernel_size=3,
                                   stride=strides, padding=1,
                                   groups=bot_channels//groups) # b*b / g
        self.conv3 = nn.LazyConv2d(num_channels, kernel_size=1, stride=1) # 1x1, c_o x b
        self.bn1 = nn.LazyBatchNorm2d()
        self.bn2 = nn.LazyBatchNorm2d()
        self.bn3 = nn.LazyBatchNorm2d()
        if use_1x1conv:
            self.conv4 = nn.LazyConv2d(num_channels, kernel_size=1,
                                       stride=strides) # c_o x c_i
            self.bn4 = nn.LazyBatchNorm2d()
        else:
            self.conv4 = None

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = F.relu(self.bn2(self.conv2(Y))) # group conv
        Y = self.bn3(self.conv3(Y))
        if self.conv4:
            X = self.bn4(self.conv4(X))
        return F.relu(Y + X)

参考

Diving into Deep Learning

Share on

Twitter Facebook LinkedIn

Shi-Feng Ren