RNN Basic and Modern Architecture

August 20, 2024 5 minute read

在分类、回归等任务中（eg. 点击率预估、图像类别预估），给定特征$X$后，预估固定的目标$y$，例如在点击率预估任务中，$y$有两种选择：点击、不点击。而现实中，我们经常有需要预估一个结构化的目标的需求，例如给定一个图片，自动描述其内容；给定一句中文，自动翻译出其英文表达；给定一段音频，自动识别出不同语言的文字表达。这种我们通常称sequence-to-sequence任务，其有两种形式。其一，对齐(aligned)，每个时间步的输入对应特定的目标(e.g., part of speach tagging)；其二，非对齐(unaligned)，每个时间步的输入和输出不是完全对齐(e.g. 语言翻译)。接下来，我们将探究处理这类问题的思路、方法和工具。

Autoregressive Model

在非结构化的预估任务中（e.g. 点击率预估），通常假设输入$X$是从某个确定未知的分布$P(X)$独立同分布采样出来。在结构化预估任务中，仍然可以假设全部序列（e.g. 全部文档集）独立同分布的从某确定未知的分布中采样出来，但是我们无法假设每个时间步的数据都是相互独立的。例如，一个文档中单词，后出现的单词通常更依赖于其前面的单词，并且时间步越近，受影响越大。因此，大多数的序列模型都不会假设每个时间步的数据是相互独立的，只需要假设这些序列数据是从一个固定分布中独立同分布采样的。因此，引出了一个最直接的问题 –> unsupervised density model (or sequence modeling):

给定一个序列的集合，预估指定序列$x_1,x_2,…,x_T$出现的概率，如何找出这个概率质量函数 $P$？

我们先考虑一个简单的问题: 如何预估$x_t$，假设我们只有一个序列集和，没有其他任何数据，能影响$x_t$的，只有时间步$t$前的数据$x_{t-1}, …, x_1$, 因此问题建模为计算条件概率分布:

\[P(x_t | x_{t-1},...,x_1)\]

虽然预估连续值随机变量的整个分布可能很困难，但预估出一个变量的值后，其他变量也可以类似预估出来。这种根据同一个信号之前时刻取值预估当前时刻取值的模型，称为自回归模型(Autoregressive model)。

实际处理时，通常只会选取时刻T之前$\tau$个时刻的值作为条件，每次预估的参数个数都是相同的，实际操作中方便处理输入；此外，模型可以维护一个表示过去状态的隐藏变量$h_t$，预估$\hat{x_t}$时, $h_t$作为输入: $\hat{x_t} = P(x_t|h_t)$，同时更新用$h_{t-1}, x_{t-1}$ 更新 $h_t = g(h_{t-1}, x_{t-1})$。计算$Loss(x_t, \hat{x_t})$，回传错误信号，更新模型。由于$h_t$不是可见变量，这类模型也称为隐状态自回归模型(latent autoregressive model)。

Sequence Model

如何计算概率质量函数$P$预估序列出现的概率？应用chain rule of probability，将序列模型（语言模型）建模分解为自回归预估的乘积：

\[P(x_1,...,x_T)=P(x_1) \prod_{t=2}^{T}P(x_t|x_{t-1},...,x_1)\]

因此序列模型完成了预估下一个词 和 预估序列出现概率的双重任务。

Markov Models

Markov condition: 序列在时间步$x_t$只依赖前$\tau$步的取值，即：去掉$\tau$步之前的时间步，而不影响预估能力。
Markov model: 满足Markov condition的模型

$\tau =1$时, first-order Markov model, $\tau =k$时, $k^{th}-order Markov model$

$\tau$越大，效果越好；随着$\tau$逐渐增大，效果增益快速降低，计算量增大。实际使用时，根据计算资源，灵活选择取值。

Measure languate model

Entroy

给定一个分布$P(x)$，其 entropy 定义为 $H[P] = \sum_{j}^{n}-P(j)logP(j)$ 。

$-Log(P(j))$用于量化观测到事件$j$时的惊讶程度，或者传输信息需要的比特数，其被称为 Information content。概率为1时, 信息量为0，概率越低，信息量越大，因为当一个低概率的事件发生时，通常能传达重要的信息。

Cross Entropy

给定数据的概率分布$P$，基于其产生的数据预估的概率分布$Q$（主观概率），交叉熵定义为关于主观概率$Q$的期望惊讶程度(surprisal)或者信息量。

$H(P,Q) = \stackrel{\textrm{def}}{=} \sum_j - P(j) \log Q(j)$

Perplexity

预测序列的n个token的平均交叉熵 $\frac{1}{n} \sum_{t=1}^n -logP(x_t \mid x_{t-1},\ldots,x_1)$。

自然语言领域，倾向使用 $\exp\left(-\frac{1}{n} \sum_{t=1}^n \log P(x_t \mid x_{t-1}, \ldots, x_1)\right).$ 作为 perplexity，衡量语言模型的性能。

最好理解perplexity的方式是将其理解为，当预测下一个token时，token真实的可选择数量的几何平均的倒数。

最好情况，当模型完美的预估目标token的概率=1，模型的perplexity等于1。
最坏情况，当模型预估目标token的概率为0，模型的perplexity趋向正无穷大。
一个位置可选择填充token的数量时词表的大小，模型没有学习的情况下，模型学到的分布应该是一个均匀分布，模型的perplexity=词表去重后token的数量。

Softmax and Cross-entropy loss

Softmax

当预估下一个位置应该取哪一个token时，词表中的所有token是我们的候选，神经网络的输出向量长度为词表大小$|V|$，输出向量中的每一个元素和词表中的token一一对应。 label向量使用one-hot方式编码，其向量长度和词表大小一致，向量目标元素的位置和词表中的token一一对应，此时我们是将分类问题当成回归问题来解决。这是可行的，但是存在一些问题：

输出向量中的元素的和不能保证等于1（我们期望其能表现的像概率一样，要预测的位置有V个token可以选择，我们需要选择出概率最大的那个）
无法保证输出向量的每个元素是非负的（概率不能看小于0）
将分类问题当作回归问题解决，对异常值更敏感。例如，假如一个人在购房和卧室数量有正相关关系，当用户购买大厦时，概率很可能会超过1。

因此，我们需要一种机制来压缩输出:

假设输出$o$是真实label的噪声版本，即: $y = o + \epsilon, {\epsilon}_{i} \sim N(0, {\sigma}^2)$。其被称为probit model。相比softmax，实际表现不算好，也不容易优化。
利用指数函数，令 $P(y=i) \approx exp(o_i)$。其满足单调性和非0要求，概率随$o_i$的增大增大；标准化后，所有可能的概率和为1。

\[\hat{\mathbf{y}} = \mathrm{softmax}(\mathbf{o}) \quad \textrm{where}\quad \hat{y}_i = \frac{\exp(o_i)}{\sum_j \exp(o_j)}.\]

注意：输出向量$\textrm{o}$的最大分量和$\hat{\textrm{y}}$中最可能的分类一一对应，不需要额外计算。

实际应用中，多个(n)样本组织在一起(minibatch)进入模型训练，$\mathbf{X} \in \mathbf{R}^{n \times q}$，每一行代表一个样本d代表输入样本的维度。假设有$q$个类别，则输出的权重矩阵 $\mathbf{W} \in \mathbf{R}^{d \times q}, \quad \textrm{bias} \quad \mathbf{b} \in \mathbf{R}^{1 \times q}$

\[\begin{aligned} \mathbf{O} &= \mathbf{X} \mathbf{W} + \mathbf{b}, \\ \hat{\mathbf{Y}} & = \mathrm{softmax}(\mathbf{O}). \end{aligned}\]

对$\mathbf{O}$的每一行计算softmax，计算时需要考虑避免对大数使用exp和log，这可能会导致数值overflow and underflow。深度学习库自动做了优化，避免自己实现。

计算softmax，避免数值稳定性问题的技巧：

减去logits中的最大值: $softmax(z) = \frac{e^{z_i - max(\mathbf{z})}}{\sum_j e^{z_j - max(\mathbf{z})}}$
减去logits中的最大值后,$o_j - max(\mathbf{o})$可能有较大的负值，由于精度受限制，导致$exp(o_j - max(\mathbf{o}))$为0。当计算$log \hat{y_i}$时，将会得到负无穷大。幸运的时，我们在计算Cross-entropy时，要计算$log(\hat{y_i})$，结合一起计算得到:

\[\begin{aligned} log (\hat{y_i}) &= log \frac{exp(o_j-max(\mathbf{o}))}{\sum_k exp(\mathbf{o_k} - max(\mathbf{o_k}))} \\ &= o_j - max(\mathbf{o}) - log(\sum_k exp(\mathbf{o_k} - max(\mathbf{o_k}))) \end{aligned}\]

这样就避免了数值overflow和underflow，上式中 $log \sum_k exp(\mathbf{o_k} -max(\mathbf{o_k}))$使用了类似LogSumExp trick

Negative log-likelihood (NLL)

假设label $Y$是使用one-hot编码的向量，同时假设 $Y$ 是独立同分布的。则给定特征$X$，最大化$Y$的似然概率为：

\[P(Y|X) = \prod_{i=1}^n P(\mathbf{y}^{(i)} \mid \mathbf{x}^{(i)})\]

机器学习中，通常优化其负对数似然形式：

\[-\log P(\mathbf{Y} \mid \mathbf{X}) = \sum_{i=1}^n -\log P(\mathbf{y}^{(i)} \mid \mathbf{x}^{(i)}) = \sum_{i=1}^n l(\mathbf{y}^{(i)}, \hat{\mathbf{y}}^{(i)})\]

损失函数 $l$ 如下，其中q为类别数量：

\[l(\mathbf{y}, \mathbf{\hat{y}}) = - \sum_{i=1}^{n} y_i log \hat{y_i}\]

上式通常称为交叉熵损失，当$\hat{y}$是概率值向量时（每个分量都在0~1之间），NLL的最小值等于0，此时模型100%的把握预测对了真实的值。当权重被限制在特定大小的范围时（事实上，收到机器精度影响，必须限制在特定大小范围内），损失值等于0的情况永远不可能发生，因为这需要要求softmax的输出为1，同时也要求对应的输出$o_i$为无穷大（或者其他$j \neq i$输出 $o_j$ 趋向负无穷大），此时即使模型可以输出为0的概率值，同时也会导致损失函数，无穷大，导致无法学习。

Connection between Softmax and CE loss

将softmax函数和交叉熵损失结合起来，简化公式，得到：

\[\begin{aligned} l(\mathbf{y}, \hat{\mathbf{y}}) &= - \sum_{j=1}^q y_j \log \frac{\exp(o_j)}{\sum_{k=1}^q \exp(o_k)} \\ &= \sum_{j=1}^q y_j \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j \\ &= \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j. \end{aligned}\]

计算损失函数关于logit $o_j$ 的梯度得到：

\[\partial_{o_j} l(\mathbf{y}, \hat{\mathbf{y}}) = \frac{\exp(o_j)}{\sum_{k=1}^q \exp(o_k)} - y_j = \mathrm{softmax}(\mathbf{o})_j - y_j.\]

注意：损失函数关于logit的梯度等价于预估分类 $j$ 概率和是否是$j$分类($\in {0, 1}$)的差值；在误差分布服从正态分布的回归任务中，梯度也等于预估值和真实值的差值。这并非巧合，在指数簇的模型中，其log似然关于logit的梯度都能用这种形式精确的表达出来。

Recurrent Neural Networks

Why use Hidden States

每个时间步token $x_t$的条件概率都依赖前 $n-1$ 个token，如果想依赖更早的token，需要增大窗口 $n$，同时参数量也会指数增加（窗口内的每个位置都有 $\mathbf{V}$ 个选择），我们需要存储 $\mathbf{V}^n$ 数量的参数。

引入隐状态 $h_t$，其存储了前t个时间步的序列信息：

\[P(x_t \mid x_{t-1} \ldots x_1) \approx P(x_t \mid h_{t-1})\]

使用$h_{t-1}, x_t$更新隐状态:

\[h_t = f(x_t, h_{t-1})\]

隐藏层是从输入到输出中间不被观测到的层，隐残层可以包含权重，也可以不包含（例如池化层），这里的权重可以理解为转换矩阵，用于将输入进行某种形式的转换。
隐藏状态是真实存在的状态，其存储了前若干个时间步骤的序列信息，可以是某个特定时间步的任何模块的输入。隐藏层则只能接受固定层的输入。

Basic RNN Architecture

组成要素：

时间步t的小批量输入: $X_t \in \mathbf{R}^{n \times d}$
时间步t的隐状态: $ H_t \in \mathbf{R}^{n \times d} $
隐状态权重矩阵: $ W_{hh} \in \mathbf{R}^{h \times h} $，用于描述如何使用前 $t-1$步的隐状态
输入权重矩阵: $ W_{xh} \in \mathbf{R}^{d \times h} $，用于描述如何使用时刻t的输入
隐状态Bias: $b_h \in \mathbf{R}^h $
输出层权重矩阵: $ W_{hq} \in \mathbf{R}^{h \times q} $, q是类别数量

Step 1: Update Hidden State:

\[H_t = \phi(X_t W_{xh} + H_{t-1}W_{hh} + b_h)\]

Step 2: Output at time step t:

\[O_t = H_t W_{hq} + b_q\]

class RNNScratch(Module): 
    """The RNN model implemented from scratch."""
    def __init__(self, num_inputs, num_hiddens, sigma=0.01):
        super().__init__()
        self.W_xh = nn.Parameter(
            torch.randn(num_inputs, num_hiddens) * sigma)
        self.W_hh = nn.Parameter(
            torch.randn(num_hiddens, num_hiddens) * sigma)
        self.b_h = nn.Parameter(torch.zeros(num_hiddens))
    def forward(self, inputs, state=None):
        if state is None:
            # Initial state with shape: (batch_size, num_hiddens)
            state = torch.zeros((inputs.shape[1], self.num_hiddens),
                              device=inputs.device)
        else:
            state, = state
        outputs = []
        for X in inputs:  # Shape of inputs: (num_steps, batch_size, num_inputs)
            state = torch.tanh(torch.matmul(X, self.W_xh) +
                            torch.matmul(state, self.W_hh) + self.b_h)
            outputs.append(state)
        return outputs, state

Grad clipping for prevent from exploding gradients

使用小学习率可以缓解梯度爆炸，但会降低训练速度
限制梯度的最大norm不超过$\theta$, $g \leftarrow min(1, \frac{\theta}{\lVert \mathbf{g} \rVert }) g$

使用Grad Clipping 会让梯度不是真正的梯度，可能会有一些副作用，但很能准确分析出可能的副作用。从实践角度看，是一个非常有用的技巧。

Backpropagation Through Time (BPTT)

Analysis of Gradients in RNN explains more detail

假设RNN模型如下：

\[\begin{aligned}h_t &= f(x_t, h_{t-1}, w_\textrm{h}),\\o_t &= g(h_t, w_\textrm{o}),\end{aligned}\]

$w_\textrm{h}$, $w_\textrm{o}$ 分别代表隐藏层和输出层的权重

损失函数依赖T时间步中计算的损失和：

\[L(x_1, \ldots, x_T, y_1, \ldots, y_T, w_\textrm{h}, w_\textrm{o}) = \frac{1}{T}\sum_{t=1}^T l(y_t, o_t).\]

计算关于隐藏层的权重的梯度：

\[\begin{aligned}\frac{\partial L}{\partial w_\textrm{h}} & = \frac{1}{T}\sum_{t=1}^T \frac{\partial l(y_t, o_t)}{\partial w_\textrm{h}} \\& = \frac{1}{T}\sum_{t=1}^T \frac{\partial l(y_t, o_t)}{\partial o_t} \frac{\partial g(h_t, w_\textrm{o})}{\partial h_t} \frac{\partial h_t}{\partial w_\textrm{h}}.\end{aligned}\]

因为 $\frac{\partial h_t}{\partial w_h}$ 同时依赖 $h_{t-1}, w_h$, 利用求导链式法则：

\[\frac{\partial h_t}{\partial w_\textrm{h}}= \frac{\partial f(x_{t},h_{t-1},w_\textrm{h})}{\partial w_\textrm{h}} +\frac{\partial f(x_{t},h_{t-1},w_\textrm{h})}{\partial h_{t-1}} \frac{\partial h_{t-1}}{\partial w_\textrm{h}}.\]

为了计算出递推式，我们做以下替换：

\[\begin{aligned}a_t &= \frac{\partial h_t}{\partial w_\textrm{h}},\\ b_t &= \frac{\partial f(x_{t},h_{t-1},w_\textrm{h})}{\partial w_\textrm{h}}, \\ c_t &= \frac{\partial f(x_{t},h_{t-1},w_\textrm{h})}{\partial h_{t-1}},\end{aligned}\]

t=0时，$a_0=0$, t>0时, $a_{t}=b_{t}+c_{t}a_{t-1}$, 因此容易计算出：

\[a_{t}=b_{t}+\sum_{i=1}^{t-1}\left(\prod_{j=i+1}^{t}c_{j}\right)b_{i}.\]

变量替换回后，得到：

\[\frac{\partial h_t}{\partial w_\textrm{h}}=\frac{\partial f(x_{t},h_{t-1},w_\textrm{h})}{\partial w_\textrm{h}}+\sum_{i=1}^{t-1}\left(\prod_{j=i+1}^{t} \frac{\partial f(x_{j},h_{j-1},w_\textrm{h})}{\partial h_{j-1}} \right) \frac{\partial f(x_{i},h_{i-1},w_\textrm{h})}{\partial w_\textrm{h}}.\]

当t取值很大时，计算量显然很大，其中的梯度连乘操作时梯度爆炸和梯度消失现象发生的根本原因。

实际使用两种方法缓解梯度爆炸和梯度消失问题：

Truncated BTPP (TBTPP): 只计算前$\tau$步的梯度, 这是一种计算真实梯度的近似。实际效果很好。主要问题是会导致模型相比长期因素，更关注短期因素的影响，这会导致模型更偏向简单、稳定的方向发展，事实上，也是符合预期的。可以认为 TBTPP 一定程度上增加了正则化。
Random Truncation (Anticipated reweighted TBTPP): 通过精心设计变长的截取长度，提供无偏TBTPP计算，详细可见论文，实际使用不多。

实际实现时，每个实际步产生的临时变量$h_t$及其梯度和换成下来用以加速计算。

Addressing grad vanish by LSTM

最早、最成功解决梯度消失问题的技术，来自LSTM网络(Long short-term memory)。其核心是一个被称为带门控的记忆单元的结构。

Gated Memory Cell

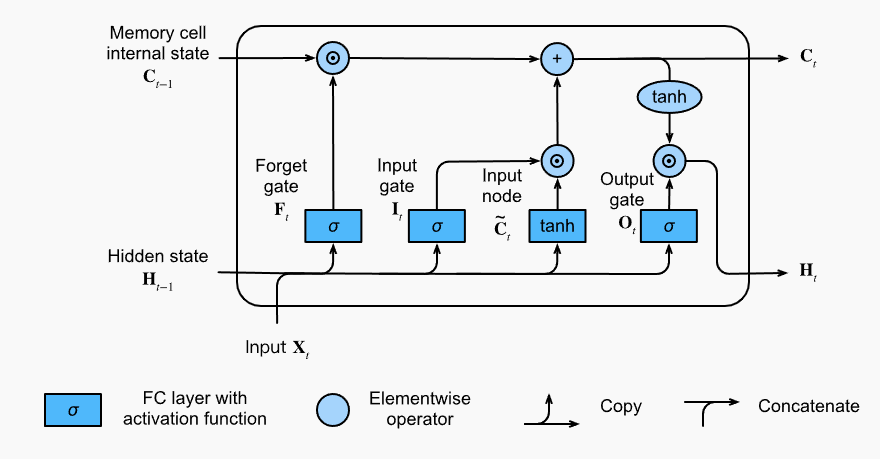
lstm-cell

每个记忆单元都有一个内部状态 $C$, 和三个乘性的门控：

输入门: 控制如何影响内部状态$C$
输出门：控制内部状态$C$如何影响隐状态输出
遗忘门：控制内部状态$C$如何更新（遗忘或更新）

因此和RNN最重要的不同就是遗忘门的设计，即如何公式隐状态的更新。

计算输入门、输出门和遗忘门：

\[\begin{aligned} \mathbf{I}_t &= \sigma(\mathbf{X}_t \mathbf{W}_{\textrm{xi}} + \mathbf{H}_{t-1} \mathbf{W}_{\textrm{hi}} + \mathbf{b}_\textrm{i}),\\ \mathbf{F}_t &= \sigma(\mathbf{X}_t \mathbf{W}_{\textrm{xf}} + \mathbf{H}_{t-1} \mathbf{W}_{\textrm{hf}} + \mathbf{b}_\textrm{f}),\\ \mathbf{O}_t &= \sigma(\mathbf{X}_t \mathbf{W}_{\textrm{xo}} + \mathbf{H}_{t-1} \mathbf{W}_{\textrm{ho}} + \mathbf{b}_\textrm{o}), \end{aligned}\]

计算输入节点：控制输入X进入内部状态$C$的信息量

\[\tilde{\mathbf{C}}_t = \textrm{tanh}(\mathbf{X}_t \mathbf{W}_{\textrm{xc}} + \mathbf{H}_{t-1} \mathbf{W}_{\textrm{hc}} + \mathbf{b}_\textrm{c}),\]

更新内部状态$C$：

\[\mathbf{C}_t = \mathbf{F}_t \odot \mathbf{C}_{t-1} + \mathbf{I}_t \odot \tilde{\mathbf{C}}_t.\]

这种设计给模型一定的自由度，学习何时保持内部状态不变，何时需要更新内部状态，何时不用内部状态。实践中，这种设计也一定程度缓解了梯度消失问题，即使序列很长，也让模型更容易训练。

计算隐状态:

\[\mathbf{H}_t = \mathbf{O}_t \odot \tanh(\mathbf{C}_t).\]

易见，计算输入节点和隐状态时，均使用tanh激活函数，保持隐状态的值域在(-1,1)之间。

但是为什么选择使用 tanh作为隐状态和输入节点的激活函数，sigmoid作为门控的激活函数？ stackoverflow、stackexchange有一些有益的讨论。

门控函数的作用是控制信息被使用的多少，例如不用或者完全使用，sigmoid的输出值域在0~1之间，符合门控函数的作用。

输入状态和隐状态使用tanh激活，个人认为不宜被值域在0~1之间的激活函数替换的。因为输入节点对隐藏层的贡献，隐藏层对于下一层输入的贡献，可能是正的，也可能是负，要表达这种含义，需要让激活函数的值域在(-1,1)之间，来表达正负贡献的作用；对于某些具体的任务，输入节点和隐藏层对下一层的贡献可能都是正相关的，此时可以选择替换。

class LSTMScratch(Module):
    def __init__(self, num_inputs, num_hiddens, sigma=0.01):
        super().__init__()

        init_weight = lambda *shape: nn.Parameter(torch.randn(*shape) * sigma)
        triple = lambda: (init_weight(num_inputs, num_hiddens),
                          init_weight(num_hiddens, num_hiddens),
                          nn.Parameter(torch.zeros(num_hiddens)))
        self.W_xi, self.W_hi, self.b_i = triple()  # Input gate
        self.W_xf, self.W_hf, self.b_f = triple()  # Forget gate
        self.W_xo, self.W_ho, self.b_o = triple()  # Output gate
        self.W_xc, self.W_hc, self.b_c = triple()  # Input node

    def forward(self, inputs, H_C=None):
        if H_C is None:
            # Initial state with shape: (batch_size, num_hiddens)
            H = torch.zeros((inputs.shape[1], self.num_hiddens),
                          device=inputs.device)
            C = torch.zeros((inputs.shape[1], self.num_hiddens),
                          device=inputs.device)
        else:
            H, C = H_C
        outputs = []
        for X in inputs:
            I = torch.sigmoid(torch.matmul(X, self.W_xi) +
                            torch.matmul(H, self.W_hi) + self.b_i)
            F = torch.sigmoid(torch.matmul(X, self.W_xf) +
                            torch.matmul(H, self.W_hf) + self.b_f)
            O = torch.sigmoid(torch.matmul(X, self.W_xo) +
                            torch.matmul(H, self.W_ho) + self.b_o)
            C_tilde = torch.tanh(torch.matmul(X, self.W_xc) +
                              torch.matmul(H, self.W_hc) + self.b_c)
            C = F * C + I * C_tilde
            H = O * torch.tanh(C)
            outputs.append(H)
        return outputs, (H, C)

GRU

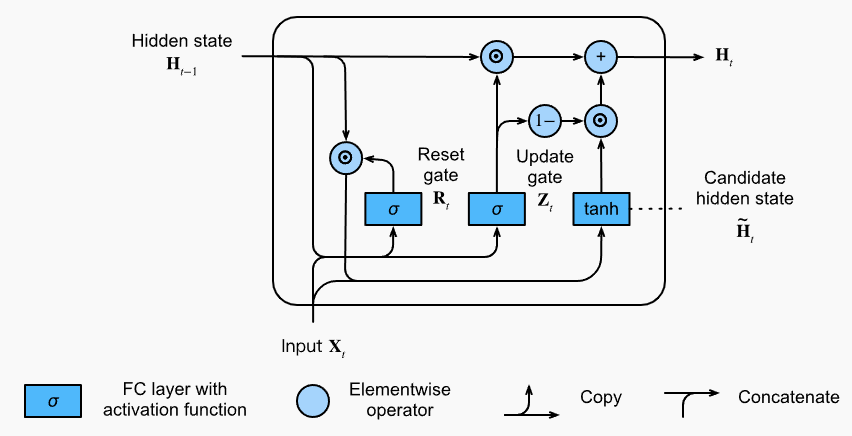
gru-cell

简化门控机制，提高计算性能，同时效果不差。

重置门(reset gate) : 控制输入的隐状态使用多少用于生成候选隐状态
更新门(update gate)：控制新的隐状态保留老的隐状态多少信息, 候选隐状态使用多少信息

\[\begin{aligned} \mathbf{R}_t = \sigma(\mathbf{X}_t \mathbf{W}_{\textrm{xr}} + \mathbf{H}_{t-1} \mathbf{W}_{\textrm{hr}} + \mathbf{b}_\textrm{r}),\\ \mathbf{Z}_t = \sigma(\mathbf{X}_t \mathbf{W}_{\textrm{xz}} + \mathbf{H}_{t-1} \mathbf{W}_{\textrm{hz}} + \mathbf{b}_\textrm{z}), \end{aligned}\]

计算候选隐状态

\[\tilde{\mathbf{H}}_t = \tanh(\mathbf{X}_t \mathbf{W}_{\textrm{xh}} + \left(\mathbf{R}_t \odot \mathbf{H}_{t-1}\right) \mathbf{W}_{\textrm{hh}} + \mathbf{b}_\textrm{h}),\]

计算隐状态

\[\mathbf{H}_t = \mathbf{Z}_t \odot \mathbf{H}_{t-1} + (1 - \mathbf{Z}_t) \odot \tilde{\mathbf{H}}_t.\]

class GRUScratch(Module):
    def __init__(self, num_inputs, num_hiddens, sigma=0.01):
        super().__init__()

        init_weight = lambda *shape: nn.Parameter(torch.randn(*shape) * sigma)
        triple = lambda: (init_weight(num_inputs, num_hiddens),
                          init_weight(num_hiddens, num_hiddens),
                          nn.Parameter(torch.zeros(num_hiddens)))
        self.W_xz, self.W_hz, self.b_z = triple()  # Update gate
        self.W_xr, self.W_hr, self.b_r = triple()  # Reset gate
        self.W_xh, self.W_hh, self.b_h = triple()  # Candidate hidden state

    def forward(self, inputs, H=None):
        if H is None:
            # Initial state with shape: (batch_size, num_hiddens)
            H = torch.zeros((inputs.shape[1], self.num_hiddens),
                          device=inputs.device)
        outputs = []
        for X in inputs:
            Z = torch.sigmoid(torch.matmul(X, self.W_xz) +
                            torch.matmul(H, self.W_hz) + self.b_z)
            R = torch.sigmoid(torch.matmul(X, self.W_xr) +
                            torch.matmul(H, self.W_hr) + self.b_r)
            H_tilde = torch.tanh(torch.matmul(X, self.W_xh) +
                              torch.matmul(R * H, self.W_hh) + self.b_h)
            H = Z * H + (1 - Z) * H_tilde
            outputs.append(H)
        return outputs, H

Share on

Twitter Facebook LinkedIn

Shi-Feng Ren